Makeup Torque Changes Your Tensile Capacity

I want to just have a torque capacity and a tension capacity for my connection. But it don’t work like that.

Last time I said that the API recommended makeup torques are arbitrary, with the important caveat that “arbitrary” is not “bad”—we wanted to pick a standard value, and we did. That standard value works pretty well, pretty often, and it’s a big boon to our industry to have an easy table in our back pocket. What “arbitrary” means is we can change it if we need to.

But that raises important questions, like why would we need to? What do we gain, and what might we lose? Questions that I’m going to answer … with an overwrought thought experiment.

Casey the roughneck stabs our pin into the box, and the spinner whips that thing around, advancing the connection into full engagement. He gets to the point where he bumps the shoulders, and (at some crazy engineer’s suggestion) he stops there. The connection is fully engaged, everything’s where it’s supposed to be, but there’s no stress at all in it. Now Grant (the crazy engineer) tells Chris (the driller) to pick the string up out of the slips. Casey and Chris exchange wide-eyed looks, Casey ducks into the doghouse, and Chris starts to pull.

What happens? We saw before that if we have zero stress in the connection, then that means there’s zero seal stress; zero seal stress means there’s zero pressure capacity. It’s going to leak as soon as we turn on the pumps.

Maybe crazy-engineer Grant tells Chris to not turn on the pumps though. (He’s got a theory, and the company man is giving him enough rope to hang himself.) We’re pulling on a connection with zero makeup torque applied … and nothing goes wrong. The connection’s fully engaged, so the threads don’t strip out or anything; the pin is capable of carrying quite a bit of tensile load without yielding.

(This is not purely theoretical. I’ve been there—a lab, not on a rig—when the techs just bumped the shoulders on an NC38 connection with a strap wrench and then pulled the thing to over a million pounds. Stronger-than-normal material, but you get the point.)

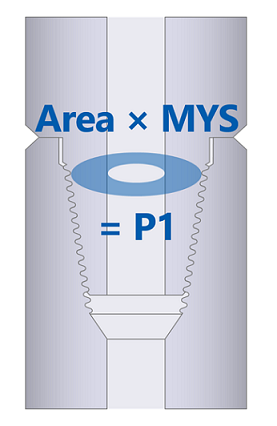
In fact, in order for the connection to fail by yielding (the pumps are still off, so we don’t care about fail-by-leaking), you’d have to yield the cross section of the pin neck. So, we figure what the cross section is at the last-engaged thread of the pin (I’ll leave that math as an exercise for the reader), we multiply that by the yield strength of the connection (usually 120,000 psi for our tool joints), et voila! 

Now we know the tensile load required to yield our pin. Let’s give it a name: Christi? Fernando? We’ll call it “P1.” (I know, “Fernando” is better, but I’m using API’s labels here, and they call it “P1.”)

So is The Honorable P1 the tensile capacity of our connection? No, remember the story—we haven’t turned the pumps on. We usually do, which would mean failure is imminent. Our current tensile capacity when we consider fail-by-leaking, which we do, is zero.

Let’s try again. Same connection, same process—stab, spin, bump the shoulders—but this time we’ll apply just a little bit of torque. (No, it doesn’t matter how much “a little bit” is, it’s a fictional story for Pete’s sake.) Because I’ve applied “a little bit” of torque, I now have “a little bit” of stress in the connection, which will translate to “a little bit” of seal stress, which means I get “a little bit” of pressure capacity.

My connection does not fail right away, so the tensile capacity is not zero. But as I pull on the connection, the pin elongates a little bit because of the tension it’s carrying. That would release whatever seal stress was there to start with—the seal stress pushes the shoulders together, but the tension pulls them apart. If I only started with “a little bit” of seal stress, then my actual tensile capacity is, you guessed it, “a little bit.”

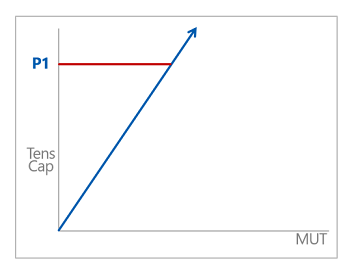
But this helps me see the way forward: if I apply more makeup torque, I get more “pre-stress” at the seal surface, so it takes more tensile load to separate those shoulders. For you visual learners:  

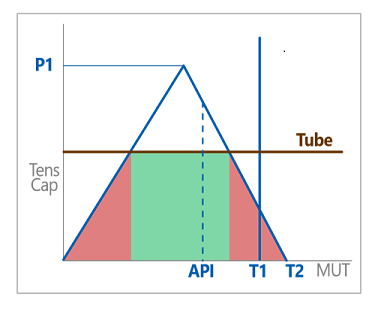
As the makeup torque (MUT) increases, the tensile load that I can apply before the connection leaks increases (blue line). However, once the shoulders are separated, then the same fail-by-yielding happens every time (red line, all at P1). It’s the same connection with no interaction from the shoulders, with the same pin and material strength, so it yields at the same load regardless of makeup torque … up to a point.

In my handy graph, you see there’s a magic number, a MUT value where, as I pull on the connection, the shoulders separate (blue line) and the pin yields (red line) at the same load (where they cross! Ain’t graphs fun?!). Clearly, on a graph lines cross only at important points. Let’s give this special MUT a name: Stephan? Jehoshaphat? API calls it “T4.” (Open challenge to API: be more creative with your names.)

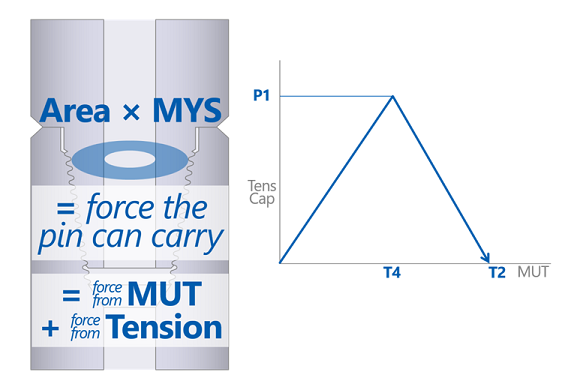
Honestly, T4 is rarely important in the sense that we want or need it. It’s important because it represents a change in behavior: if I apply a makeup torque less than T4, the connection fails in tension by leaking, as we saw. But if we apply more than T4, the pin is going to yield before we get a chance to separate the shoulders. T4 is where we switch failure mechanisms from fail-by-leaking to fail-by-yielding.

But now that we haven’t separated the shoulders, one of my basic assumptions about P1 is wrong. Now the pin isn’t just carrying string weight, it’s also carrying some of that “pre-stress” from makeup. Remember that the pin carries tensile stress from two different sources: both string tension and makeup torque (the helix of the thread causes torque to pull the pin down into the back of the box, creating tensile stress in the pin).

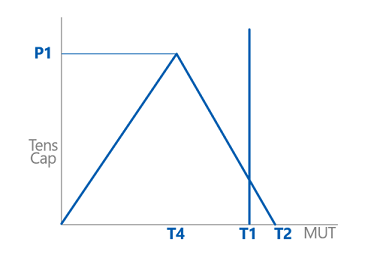
So, when the shoulders get a chance to separate, the way they do when the MUT is less than T4, all the pre-stress is released. But from T4 on, more makeup torque is going to mean less string weight before we get to failure. In fact, there’s a point where pure makeup torque (zero tension) causes failure; API calls that “T2.” (Bo-ring.)

“Wait! Grant! You forgot the box! How does makeup torque affect the box capacity?”

It doesn’t. Well, not for tension, anyway. Boxes, at least our boxes in our industry made in any reasonable size out of solid material (not damaged somehow), do not fail in tension. The taper in the threads means the tensile “weak” section is massively stronger than the pin will ever be, so we don’t even think about box tensile capacity. 

Box torsion capacity is pretty straightforward to calculate, just the amount of torque it takes to cause yielding in the box face / counterbore area, and that’s not going to change. It’s just a vertical line named “T1” on my rapidly-expanding graph.

So, your connection tensile capacity is a function of the amount of makeup torque you apply, and the exact failure type we expect changes depending on the regime we end up in on the connection combined load curve I’ve been building. It all seems kind of complicated, but there are apps that’ll help you out.

However, to reward you for reading this far, I’m now going to make your life much, much easier: 

See? See!? If I compare typical API tool joint connections to the typical tube they’re typically welded to, and then I apply the typical API makeup torque … the tube is weak in tension!

Mayhaps you don’t see why that’s so exciting. Tube tensile capacity is easy to find: a one page table in DS-1 Volume 2 takes care of all standard NWDP sizes, weights, and grades, with four different inspection classes. It’s just a number, and it doesn’t depend on the makeup torque I apply to the connection (obviously).

The torque capacity of my connection is not the yield torque, like T1 or T2; it’s the makeup torque I apply. I don’t want to make up a connection downhole (more likelihood of galling and damage), so whatever torque gets applied at the rig floor is the torque capacity of the connection, and usually the drill string (the tubes are typically stronger in torsion than the makeup torque).

So despite all this graphing and thought-experimenting, usually your tension capacity is one easy-to-find number (the tube tensile capacity), and your torsion capacity is one easy-to-find number (the API-recommended makeup torque). Easy!

“Why, Grant, why did you go through all that other crap if that was the answer!?!”

Because sometimes you’ll want to do non-typical things. If the string you’re using doesn’t have enough torque capacity (i.e. the API MUT is less than the drilling torque), you could rent an expensive string with fancy proprietary connections. Or you could look at the graph and see if 10%, 15% higher might work.

So understanding how your connections work can save you money. (Wow, talk about burying the lede.)