Bendy Tubes, a Brief Historical Sketch
Way back in 1960, Dr Arthur Lubinski (the Great) wrote a paper entitled “Maximum Permissible Dog-Legs in Rotary Boreholes.” In it he deals with several different problems that crop up because of kinks in our holes, including fatigue and heat checking. As part of that, he spends the appendix deriving equations that will tell you the maximum curvature you should allow in your pipe.
I’m happy as a pig in mud tracing the development of our industry knowledge through technical publications purely for the delight that it brings, but in this particular case I’ve got a purpose: that paper, and some related works, are the basis for the information given in the old API Recommended Practice 7G on “limitations related to hole curvature.” I’m excited that I’m a part of the work group that’s looking to update the last bit of RP7G into a new standard RP7G-3, and I volunteered (I think that’s how it happened, anyway) to look into rewriting the hole curvature chapter.
Back to Arty the Great: the 1960 paper is pretty thorough in its treatment of how curves might break things. A lot of time is spent on fatigue in drill pipe, a little bit on forces on the tool joint, and some on drill collar fatigue. There are corrections for limitations in survey tools, and considerations for smooth vs abrupt curves. There is then an extensive (and exciting!) appendix that shows the derivation of all the math (I love derivations!) used in the paper’s main body to reach the conclusions presented. It’s good stuff.
As awesome as that paper is, though, there’s a great deal that I disagree with. Some of that is related to further industry experience and development (the survey-tool limitations are fairly dated, for instance, though it would be a mistake to assume your surveys are always gospel truth). Most of my concern comes from the way he deals with fatigue. He uses what we DS-1 engineer-types tend to call an “endurance limit” model—we find the stress level for a given material below which you will never have a fatigue failure. That’s not unexpected; most engineers default to that where fatigue is concerned, largely because it’s what they teach us in college. But even the hallowed Shigley book has some fine print that bears remembering: if you’re in a corrosive environment—and we’ll call that “real life” in the drilling world—there is no endurance limit.
Thus, the basic assumption that Lubinski worked with is wrong, and I think the history of our industry has shown it to be not helpful. Your tools will break eventually; your job is to minimize your risk of downhole failure, not pretend it’ll never happen if you just check the right box.
Still, in trying to apply that incorrect assumption, good old Art developed and solved equations that will allow us to calculate the stresses involved when we bend our drill pipe around a curve, like:
(Don’t be scared, just look up what a tanh is, remember what your algebra teacher told you, and you’ll be fine.)
There’s a problem, though: c' isn’t stress, it’s weight-corrected curvature, because that’s what Arty was looking for. I’m not, so I need to dig into the derivation process (squee!) to turn that bad boy into something helpful to me.
Luckily, in my algebraic flailings I had an answer key, at least at the beginning. In our original work on Curvature Index (now given in DS-1 Volume 2), calculating tube stress under bending was step one. So Lubinski’s paper was referenced in the appendix, with a reformulation of the result that gives moment and stress as a result of curvature and tension, not the other way around.
Two things were still missing. Number one, I was looking for an expression for the side forces as well as the stresses. Art hadn’t helped me out a lot there; he assumed that the tool joints were usually the only things touching (which is mostly true, except when it’s not). That leads to a really simple version of the side forces at the tool joints, but no help in the tube-touching cases.
But Art came through later: he wrote a paper in 1977 where he revisited his work with reference to Range 3 drill pipe. Longer tubes are more likely to touch the wall, so he went back through the derivation process and was clearer and more explicit about those cases where the tube touching the wall was a more normal occurrence.
This led to the second missing thing: my understanding of what’s going on. Up to that point, I had blithely read past the assumptions that the pipe touches the wall at one point, because touching at one geometric point with no dimension to it is impossible, obviously. But the Range 3 paper made it clear that there were three separate categories of tube contact:
- No tube contact, just the tool joints touching the wall. (I’m good with that.)
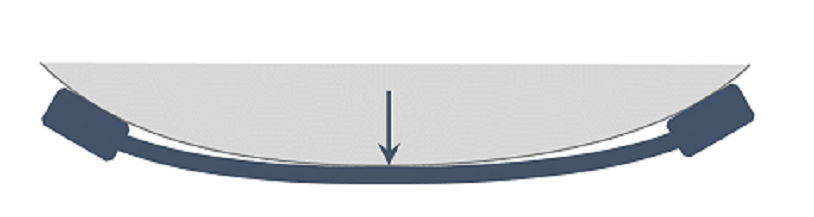
- Tube contact “at one point” in the middle of the tube. See, I ignored it, but it’s important to realize that you’re assuming all the force comes from the one place. The fact that it’s not possible on a small scale doesn’t mean that it’s not a reasonable simplification on a large scale, and it becomes an important distinction when you consider the last possibility.
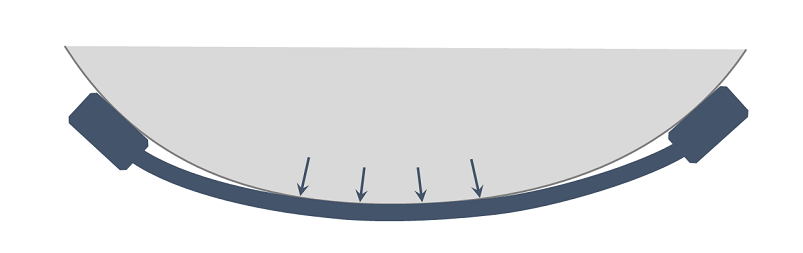
- Tube contact along a “patch” surrounding the middle of the tube. Here the tube conforms to the wall curvature along some length, and that’s obviously a different animal. (It was this one that I missed entirely, as you might have guessed.)
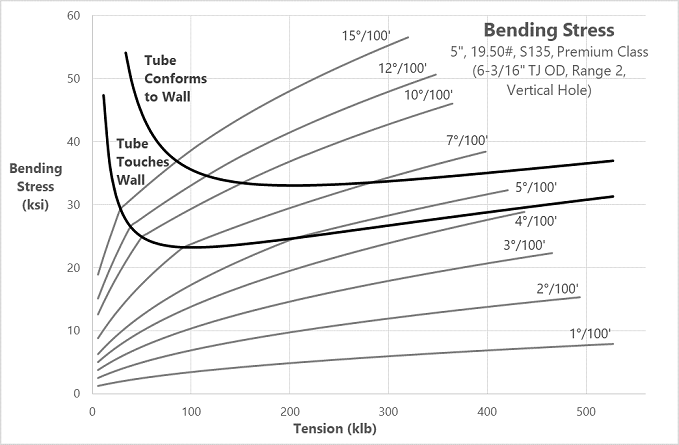
Now that Lubinski has straightened me out (and I’ve gotten some practice with hyperbolic trig identities), I can describe both the stress and the side forces in my drill pipe tube, no matter the condition it’s in. In fact, I can know what condition it’s in! I can even draw pretty graphs to describe things:
And really, what makes you look like an accomplished, intelligent engineer more than pretty graphs? Hmmm?